Just a Battery?
"Capacitors are like batteries, mostly."
Well, despite the general confusion around capacitors, this statement holds true: Capacitors charge, discharge, and store energy in between. They’re actually simpler than batteries in some ways – for example, the energy stored is not transferred into chemical energy. Everything stays in pure physics.
Capacitors are also less complicated in their physical design: unlike a battery, which consists of myriad extremely thin layers (the more layers present, the higher a voltage difference possible), a capacitor is merely a sandwich: Two conducting plates, with a non-conductive "dielectric" wedged between them. This dielectric blocks the flow of electrons between the two plates, allowing a difference in charge to build up between them. This difference in charge creates an electric field which stores our energy. Let's look at a simple circuit:
Close the switch, and the voltage over the capacitor gradually increases to match the emf. of the cell. But what actually passes through the capacitor? Ideally, nothing. But current can still be observed while the capacitor charges or discharges.
Capacitor Charging Current
"Is there a leak in my capacitor?"
Capacitors are counterintuitive from the perspective of a student who has only done GCSE-level circuitry, because they don't actually have electrons flowing through them. What instead happens is the electrons collected on one plate create an electric field, repelling electrons from the far plate, and causing the appearance of a temporary current. However once the capacitor has reached an equilibrium, this current ceases to be observed.
Capacitor leakage is also another thing sometimes encountered, where the dielectric doesn't fully insulate the capacitor, but we can ignore it for the most part.
We now know that capacitors store electrical energy and block current (yet still appear to allow some through when charging), but we haven't got to the fun bit yet.
Discharging
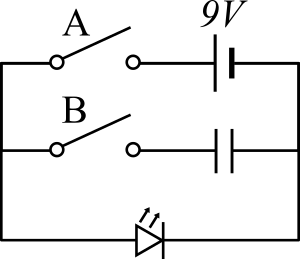
To demonstrate how discharging a capacitor works functionally, I'll need to add a few more elements to the diagram:
Firstly, let's look at the circuit with switch B open (i.e. no functional capacitor in the circuit): Switch A closes, the LED turns on. Open switch A again, the LED turns straight off.
Something more interesting happens if we close switch B, and introduce the capacitor to the circuit: Close switch A, and the LED flashes on. Open switch A, and you can even disconnect the battery – the LED will remain on for a few seconds, and dim to nothing rather than blinking off immediately.
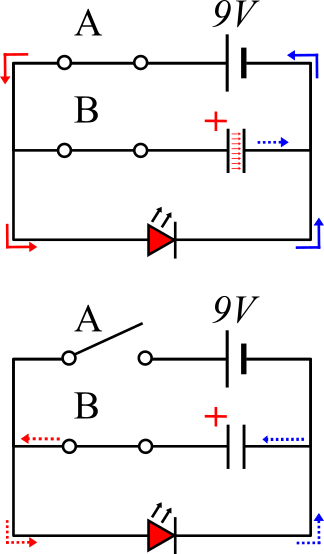
So, what happened? I'll put some arrows on the diagram to help.
In the first state, the current flows as expected – continuously through the LED, and temporarily as the capacitor charges. The voltage across the capacitor increases as it stores energy. Then, when switch A is opened, the capacitor discharges: it acts like a cell, and creates a current which passes back through the circuit, keeping the LED active until the stored energy is expended. The thing to watch out for is that the current is produced backwards, but if you consider the presence of the dielectric (insulator), then that should be fairly intuitive.
Equations and Definitions
"What even is a Farad, anyway?"
Much like resistors have their own unit, the Ohm, capacitors have the Farad. A Farad is defined as the capacitance which stores a Coulomb of charge over one Volt of potential difference – the higher the capacitance, the more charge the capacitor holds, so the more energy is packed into it at full capacity.
It's worth noting 1 Farad is much larger than most capacitors, and you're more likely to come across the milli- or micro-Farad in real-world applications.
Also, the capacitance can be worked out from one or two permeability constants (more on those another time), the area of the plates, and the distance between them, respectively. The epsilons here are those constants.
Capacitor addition
The final thing that struck me as odd about capacitors is that they add together oppositely to resistors: in parallel, they add directly, and in series they add reciprocally!
If you give parallel circuits a bit of thought it makes sense – the same voltage across three identical capacitors yields thrice the charge.
Series addition is a bit stranger – three capacitors in series would have a third of the voltage each, and re-arranging for V=Q/C we can see the sum of Voltages on a branch in a circuit is the sum of “Q/C”s, and since the charges are identical for each capacitor in a branch, you can cancel them out and see the reciprocal of summed capacity is the sum of reciprocal capacities.
Some Extras
Capacitors are extremely important in circuitry – most circuit boards have a little lentil or cylinder which is a capacitor of some variety. Moreover, different dielectric materials have different properties and are used for different purposes:1
Air: Often used in radio tuning circuits
Mylar: Most commonly used for timer circuits like alarms and counters
Glass: Good for high-voltage applications
Ceramic: Used for high frequency purposes like antennas, X-ray and MRI machines





42